Skip to main content

Mass defect, packing fraction and binding energy.

 Mass defect, packing fraction and binding energy:

It was assumed that mass of the nucleus is equal to the mass of its constituents (i.e protons and neutrons). But experimentally it was found that the actual mass of the nucleus is less than the theoretical mass. Thus, the difference between the theoretical mass and experimental mass is called mass defect i.e
∆m={[Zmₚ + (A-Z)mₙ] - M}
Where mₚ= mass of proton
             mₙ= mass of neutron
              M= actual mass of nucleus
               Z= atomic number
               A= mass number
The ratio of mass defect and mass number (A) is called packing fraction (f)
f = ∆m/A
Thus packing fraction is the mass defect available per nucleon.
The packing fraction explains the stability of the nucleus. The packing fraction may be positive, negative or zero. The positive value of packing fraction indicates that the nuclei is unstable while the negative value of packing fraction indicates that a fraction of nucleus mass has been converted into energy to form a stable nucleus.
The variation of packing fraction (f) with mass number (A) is shown in fig below.
The variation of packing fraction (f) with mass number (A)
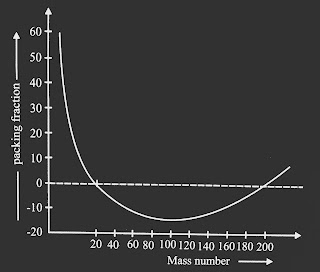The variation of packing fraction (f) with mass number (A).

To account for the difference in mass, the mass energy equivalence is used i.e
E= ∆mc²
The energy equivalent to the mass defect is called binding energy. Thus binding energy is the energy required to bind protons and neutrons to form the nucleus. Binding energy is also the energy require to break up the nucleus in order to split up into its constituents.
B.E = ∆mc² ={[Zmₚ + (A-Z)mₙ] - M}c²
The energy require to release a nucleon from the nucleus is called binding energy per nucleon and is given as
binding energy per nucleon
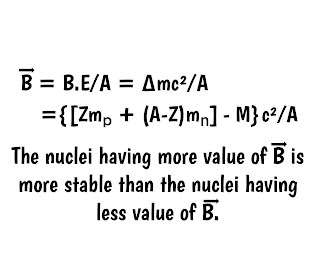Binding energy per nucleon 

The variation of binding energy per nucleon with mass number is shown in fig below.
The variation of binding energy per nucleon with mass number
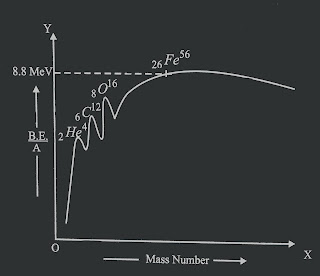The variation of binding energy per nucleon with mass number.

The characteristics of these curves are

1)B.E/A for light nuclei (eg D²,H³) are very low.
2) For A upto 20, B.E/A increases with increase in A. The curve shows variation upto atomic number 16. The nuclei ₂He⁴, ₆C¹², ₈O¹⁶ have higher B.E/A values then their neighbouring nuclei because they are considered to possess magic number i.e the mass number divisible by 4. Such nuclei have even atomic number and even n(number of neutrons).
3) B.E/A is maximum for the mass number 56 i.e 8.8 MeV. Also for A in the range 40-180 have B.E/A nearly 8.5 MeV.
4) B.E/A decreases to about 7.6 MeV/ nucleon for higher mass number A upto 238.
This decrease in B.E/A causes decrease in nucleus stability. Such nuclei disintegrate with the emission of 𝛂,𝜷 and 𝛾 rays. Such nuclei are called radioactive nuclei.

Comments

Post a Comment

Popular posts from this blog

Different kinds of beta decay.

 Different kinds of beta decay 1) Negative beta decay process: When there is excess number of neutrons in the nucleus, the neutron is converted into proton with the emission of electron and antineutrino particle and this process is called negative beta decay process. Negative beta decay. 2) Positive beta decay process: When there is excess number of protons in the nucleus, the proton is converted into neutron with the emission of positron and neutrino particle and this process is called positive beta decay process. Positive beta decay. 3) Electron Capture: When there is excess number of protons in the nucleus, sometimes the nucleus will absorbed the nearby electrons in the nearest electron orbital emitting neutron and a neutrino and this process is called electron capture. Electron capture. 4) Inverse beta decay: Inverse beta decay. Thus such kind of reaction in which neutrinos are absorbed to create some sort of beta decay is called inverse beta decay. Inverse beta decay confirm t...
Post a Comment
Read more

LS coupling and jj coupling.

 Total angular momentum: The total angular momentum of an electron is the sum of the orbital angular momentum and spin angular momentum of the electron i.e Coupling Scheme Since an atom consist of large number of electrons having different orbital and spin momenta, Coupling scheme is necessary to obtain the resultant orbit and spin momenta of atom as a whole. There are two types of coupling scheme namely 1) LS Coupling 2) JJ Coupling. 1)LS Coupling: In this coupling the 'l' vectors of all electrons combine to form resultant 'L' vector and all the 's' vectors of these electrons combine to form resultant 'S' vector. Then the 'L' vector and 'S' vector undergoes vector addition to give resultant 'J' vector which represents the total angular momentum of an atom. Symbolically LS coupling is represented as This type of coupling is governed by the following principles: 1) All the three vectors (L,S and J vectors) are quantized. 2)L is an ...
Post a Comment
Read more